home..

Lecture 10_ regulatory motifs

zying / February 2023 (385 Words, 3 Minutes)

Lecture 10: Regulator Motifs Discovery

Features

• turned on/off response to changing environment
• no direct addressing: genes contain sequences of motifs (tags)
• specialized protein (TF) recognize these tags
• motif has many different class (enhancer, promoter, splicing…)
• not limited to DNA sequences (spicing signals, Domains and epitopes at protein level, recurring patterns at physiological level…)

  Regulator structure to recognize motifs

• proteins chemical properties can recognized DNA fregments (don’t need open DNA)
• 3D topology dictates specificity (fully constrained pos or ambiguous/degenerate pos)
• other types of recognition (micro RNA, Nucleosomes, RNAs structure)

  Infomatics perspect of motif

• summary information
• integrate many pos
• measure of information

(generative model)

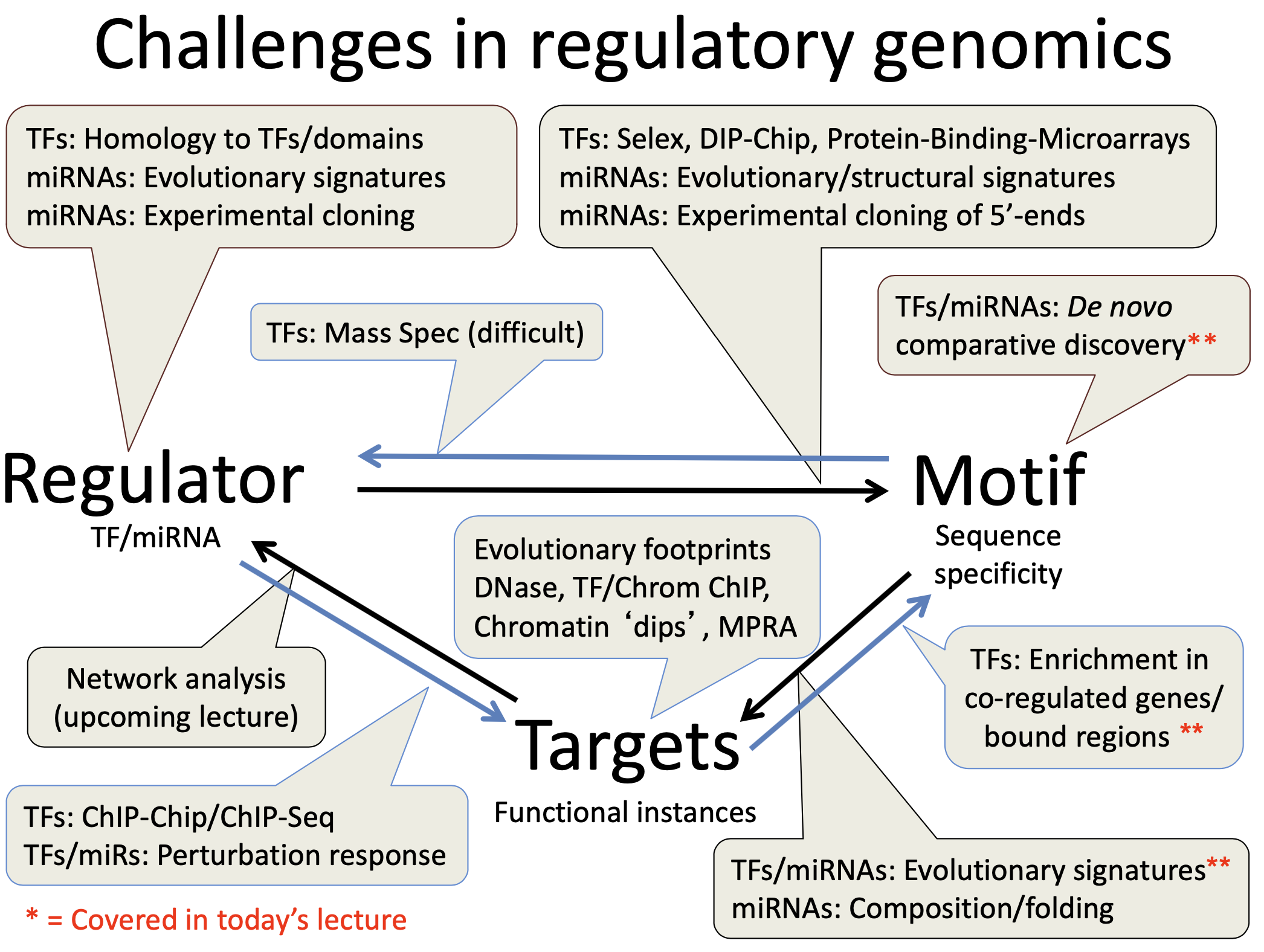
Challenges of motifs discovery

• short (6-8 bp), sometimes degenerate
• can contain any set of nucleotides
• Act at variable distance (upstream of downstream)

General thoughts of motifs discovery

• Two assumptions about the data
  • assume no pairwise correlations between bases (each base is independent) [the risk of overfitting data]
  • all motifs have fixed lengths
• methods for motif discovery
  • region-based (EM, Gibbs sampling, greedy algorithm…)
    • local alignment
    • find non-random seqences
    • reduce the search space by applying prior knowledge
    • conserved blocks
    • examine the requency of kmers
    • probabilistic methods
  • genome-wide (conservation-based)
  • In vitro/trans (protein domains): based experiments

Expectation maximization

Key idea in EM

• Starting positions<->motif matrix

  Basic Iterative Approach:
  Given: length parameter W, traning set of sequences
      	set initial value for motif
      	do 
        	-> re-estimate starting-position from motif
        	-> re-estimate motif from starting-position
      	until convergence
      	return: motif,starting positions
  

• EM is a deterministic algorithm: dependent on the initial starting points, maybe converged in local max but not global
• rerun the algorithm with different initial starting positions to try reduce the chance of converging on local max (MEME-Multiple EM for motif Elicitation)

  The E step: estimating $Z_ij$ from the PWM (profile matrix)

• Initialization (generate an initial probability weight matrix)
  • can initialize the PWM by choosing starting locations randomly
  • if there is 0 probability, it is generally good idea to insert pseudo- counts into your probabilities
  • keep a background distribution
• Expectation (generate a vector $Z_ij$)
  • calculate $Z_ij$using Bayes’ Rule (can’t comprehense clearly)

M step: Finding the maximum likelihood motif from starting positions $Z_ij$

• Maximization
• Repeat
  • to measure how much each element in the PWM changes after step max is a possible way to test whether the profile matrix has converged

    Gibbs Sampling: Sample from joint $(M,Z_ij)$

• Sampling motif position based on the Z vector
  • Initialization
  • Remove
  • Update
  • Sample
  • Iterate
• More likely to find global maximum, easy to implement

De novo motif discovery

Motivation for de novo motif discovery

• TF and centric approaches are not comprehensive and are biased
• generally require TF (antibody to factor)
• De novo using conservation is unbiased, but can't match motif to factor and require multiple genomes

  Using genome-wide conservation

Validation of discovered motifs with functional datasets

Evolutionary signatures for regulatory motifs

De novo Dissection and confirmation of regulaory regions

#

Others

Possibly deprecated stuff

Comparing different Methods

OOPS, ZOOPS, TCM

Motif Representation and Information content